Tapered holey fibers for spot-size and numerical-aperture conversion
Citation
Tapered Holey Fibers; G.E. Town and J.T. Lizier
Keywords
- Holey Optical Fiber
- Tapered Fiber
- Adiabatic Tapering
- Spot Size Conversion
- Numerical Aperture Conversion
- Effective Index Model
- Finite-Difference Time-Domain (FDTD)
Brief
Adiabatically tapered holey fibers have the potential to perform substantial scaling and reshaping of guided mode-field distributions with low loss, and without the problems associated with standard step-index fiber tapers.
Summary
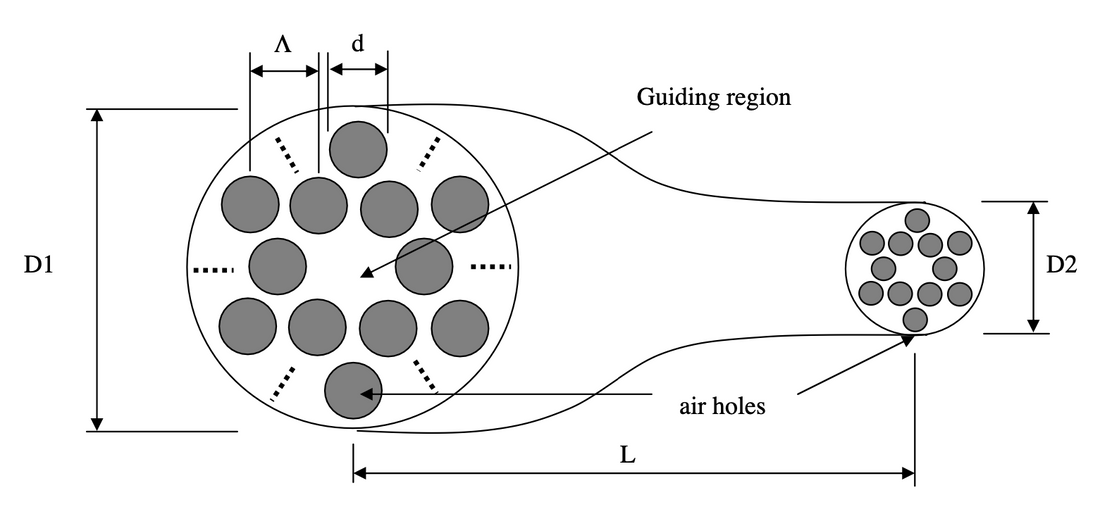
Adiabatically tapered holey fibers (HFs) are potentially useful for converting the spot size and numerical aperture in optical fibers. A tapered HF is a holey optical fiber with gradually changing dimensions. This gradual change minimizes losses from reflection and radiation, allowing for broadband impedance conversion and scaling of modal field distributions. HFs guide light through total internal reflection. The absence of a hole in the fiber forms a core, while the surrounding array of air holes creates a low effective index cladding.
A major problem with standard step-index fibers (SIFs) is their inefficiency in coupling to things like integrated optical devices, waveguides, and semiconductor devices. This inefficiency is due to a mismatch of the modal field distributions and changes in the effective index or wave impedance. While a standard method to reduce coupling losses is to use an adiabatic transition in waveguide structure (e.g. tapering), the weak guidance this provides usually results in multimode guidance or unacceptable loss.
HFs, however, have the potential to overcome the problems associated with SIF tapers and perform substantial scaling and reshaping of guided mode-field distributions with low loss. The effective normalized frequency parameter of an HF does not scale linearly with the hole pitch or size of the waveguide as the effective index of a holey cladding is wavelength dependent. As a result, an HF may be designed to remain single mode over a wide range of wavelengths. For a fixed wavelength, the size of the waveguide could be scaled significantly and still remain single mode. The numerical aperture and effective index of the guided mode could also vary significantly under tapered conversion. Tapered HFs would be effective in both directions.
The authors present finite-difference time-domain (FDTD) calculations for a down-tapered HF, showing that large spot size conversion factors are obtainable with minimal loss using short optimally shaped tapers. The authors used FDTD simulations of electromagnetic wave propagation in the axially nonuniform holey fiber waveguide to determine the transmitted and reflected fields. The authors conclude that tapered HFs have the potential to provide efficient coupling between a range of optical components. Using FDTD modeling, they demonstrated significant spot-size reduction in down-tapered holey fiber. From effective index theory, they also expect a significant increase in numerical aperture. They expect that up-tapers will be similarly effective for spot size expansion and numerical aperture reduction. The authors also expect similar conclusions to apply to any other waveguide with a periodic cladding structure.
Origin: https://lizier.me/joseph/publications/2001-TaperedHoleyFiber.pdf
